Basic statistics mathematics provides basic statistical quantities of the signal, such as RMS, Average, Min, Max, Sum, Peak, … , where those statistical functions are shown as an Output channel.
We add a new Basic statistic with adding it under Add math, as it was described before or we can adjust the existing ones with click on the Setup button on the upper right corner of already activated Basic statistics line. In both cases following will open:

Image 3: Basic statistics setup window
According to the picture above, in general we can divide Basic statistics setup window in four major parts:
| 1. | Input | Under Input group you can select desired input channels for which you want to calculate desired statistics. The statistics support multiple input channels. |
| 2. | Output channels | Here it can be selected which statistics need to be calculated. Those will be then shown as separate output channels. |
| 3. | Calculation type | In the Calculation type group you can define parameters for calculation. |
| 4. | Output | Output area offers a quick preview of calculated statistics on a selected Input, which will be outputted as a channel, based on selected options under Output channels and Calculation type. |
Output channels - Statistical functions
To select statistical function simply click (check) on the box beside its name on Output channels section:
 Image 4: Calculation Output channel options
Image 4: Calculation Output channel options
- RMS will calculate the root mean square value of the signal.
- Quadratic RMS is similar to the RMS, except all the values are double squared and summed.
- Median is the numerical value separating the higher half of a data sample from the lower half.
- Average will calculate the average or middle point.
- Peak is the maximum deviation of the signal from the average value.
- Peak-peak is the difference between the minimum and maximum.
- Crest factor is the ratio between the peak and RMS value. Crest factor gives an impression about the spikes in the signal. Pure sine waves have a crest factor of 1.41.
- Sum provides the sum of all acquired values in respect of the selected calculation type (sample or time dependent).
- Minimum will calculate a minimum value of the signal for the specified period.
- Maximum will calculate a maximum value of the signal for the specified period. This is very intensive operation and therefore unavailable in Running mode.
- Time of minimum calculates exact time of minimum value.
- Time of maximum calculates exact time of maximum value.
- Variance is indicating how possible values of a signal are spread around the expected value.
- COV (coefficient of variation) is normalized measure of dispersion of probability distribution. It is calculated as ration between standard deviation and the mean.
- Standard deviation is a measure of the spread of the values of the signal away from its mean, measuring how widely spread the values in a data set is. If the data points are close to the mean, then the standard deviation is small (if all the data values are equal, then the standard deviation is zero).
Calculation type
In this section five basic calculation types will be described:
- Block based,
- Running,
- Single value,
- Triggered blocks and
- Start-stop blocks.
Time and Sample based calculation
Before we jump into calculation types we need to mention that Block based and Running calculation type are calculated according to the specified Time interval or numbers of Samples.

Image 5: Time based and Sample based options for calculation
Time based (in seconds) defines the time interval for calculation. 0,1 second in our case means that it will calculate the statistical quantities in 0,1 second interval. Therefore the resulting channels will have an update interval of 0,1 second.
With time based calculation each signal is recalculated to a synchronous sample and then each of those synchronous samples is used as an input element for statistics calculation.
Sample based (number of samples) defines number of samples used for calculation, so resulting channels will have an update interval of defined sample block size. It is important to know that every single sample is used as an input value for statistics calculation.
Asynchronous signals are not interpolated, in fact their each value is deployed to the next sample.
Examples:
- Single value, Sample based calculation:
If you have only two samples in a measurement and their values are 5 and 10, the Single value average for a Sample based calculation will equal 7.5 and it is calculated independently of time or when those two samples were acquired.
- Single value, Time based calculation:
In this case the calculation is based on time, so the average can be anywhere between 0 and 10. Average now depends of each sample's time duration and it takes into account when the signals were acquired. So if we have in 10 seconds long measurement two samples acquired, where one sample has a value of 5 at 2 seconds and the other has a value of 10 at 4 second as it is shown on the Image 6, the Single value average will equal to 7.
 Image 6: Single value average of a time based calculation explanation
Image 6: Single value average of a time based calculation explanation
Block based
Block based calculation calculates the statistical quantity based on a specific time interval defined by the block size.
 Image 7: Block based calculation type window
Image 7: Block based calculation type window
Block size you can define by time or sample.
Overlap is useful when we need a specific time interval, but still want to have a higher update rate of the resulting channels. Overlap defines (same for as FFT averaging) how much 'old' data is taken into account for the next calculation. This increases the result update rate with the same number of lines. It can be defined in percent or as absolute value.
 Image 8: Overlap definition window
Image 8: Overlap definition window
In this case on the picture, the quantities will be updated in 0,1 second interval with 50% overlap. It means that the second block will not be calculated at the end of the first block, but half of the block before that. So the first block will be calculated from 0 to 0,1 second, second one from 0,05 to 0,15 second, third one from 0,1 to 0,2 second and so on.
Running
Running calculation is an extreme version of overlapping. The second block is calculated after one sample after the first block. Block size has the same meaning as for block based calculation.

Image 9: Running calculation type window
With this method, we can only calculate RMS, Average, Quadratic RMS, Variance and Standard deviation statistical functions, because all others would be too intensive (especially minimum and maximum while all others relate to those two).
Single value
Single value is the simplest calculation and has no settings. It will output only one value at the end of the measurement. The result will be updated also during the measurement, but only the final value will be stored in the data file.
 Image 10: Single value calculation type window
Image 10: Single value calculation type window
Triggered blocks
Triggered blocks option calculates the statistical value based on a specific trigger event. The calculation begins at the start of the acquisition. When a trigger event is recognized, it stops the first calculation, writes the statistical value with its timestamp and then starts to calculate a new value. We can define any channel as the trigger channel and the settings for the trigger condition are the same as the alarm or storage triggers.
 Image 11: Triggered blocks calculation type window
Image 11: Triggered blocks calculation type window
Start/Stop blocks
Start/stop blocks option calculates the statistical value starting at a specific trigger event. When an event is recognized, it starts to calculate. When a stop condition is recognized, then the value is written to the resulting channel with the timestamp of the stop event. It will wait with the calculation until the new start event is recognized. The start and stop channel can be any channel, also a different one and the trigger condition have the same options as the alarm or storage triggers.
 Image 12: Start-stop blocks calculation type window
Image 12: Start-stop blocks calculation type window
![]()
 Image 2: Statistics and Counting can be find in Add math drop-down window
Image 2: Statistics and Counting can be find in Add math drop-down window


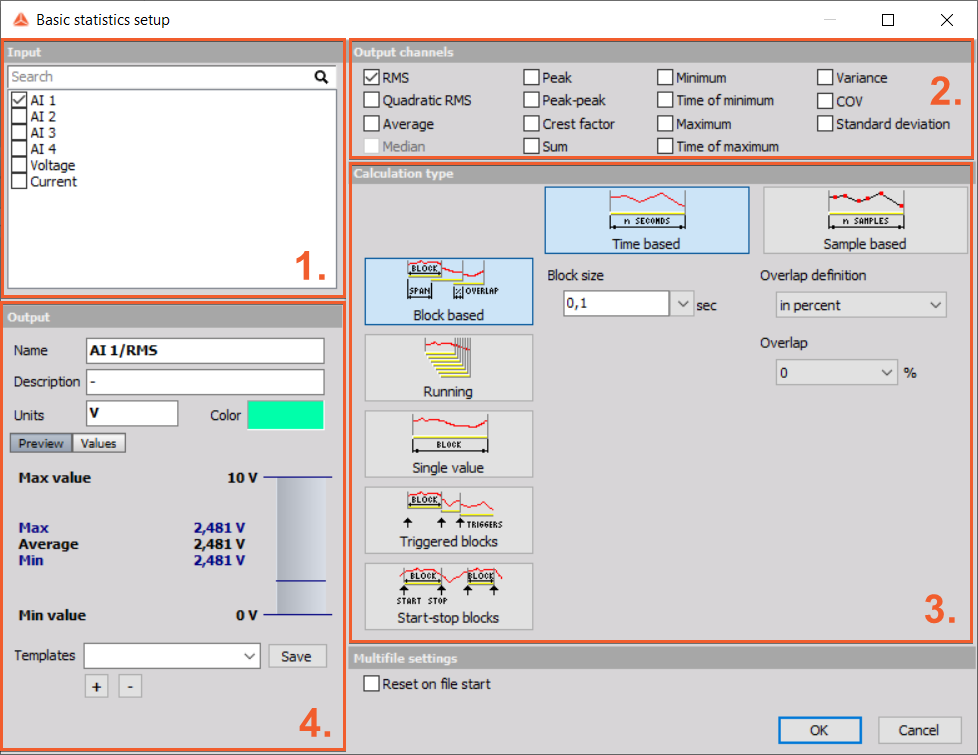


 Image 6: Single value average of a time based calculation explanation
Image 6: Single value average of a time based calculation explanation Image 7: Block based calculation type window
Image 7: Block based calculation type window




 Image 13: Array statistics setup window
Image 13: Array statistics setup window Image 14: Array area definition
Image 14: Array area definition Image 15: Classification setup window
Image 15: Classification setup window Image 16: Calculation type window for Classification
Image 16: Calculation type window for Classification Image 17: Class definition for Classification
Image 17: Class definition for Classification Image 18: Histogram types
Image 18: Histogram types Image 19: Statistics and Distribution windows
Image 19: Statistics and Distribution windows Image 20: Histogram shown on 2D graph
Image 20: Histogram shown on 2D graph Image 21: Counting setup window
Image 21: Counting setup window Image 22: Counting setup definition
Image 22: Counting setup definition Image 23: Local extreme detection
Image 23: Local extreme detection
 Image 25: Visualization setup
Image 25: Visualization setup