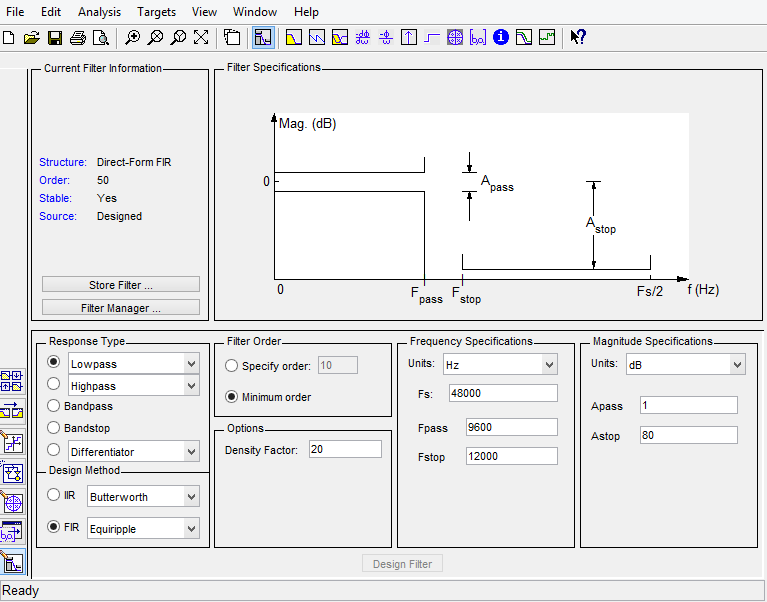
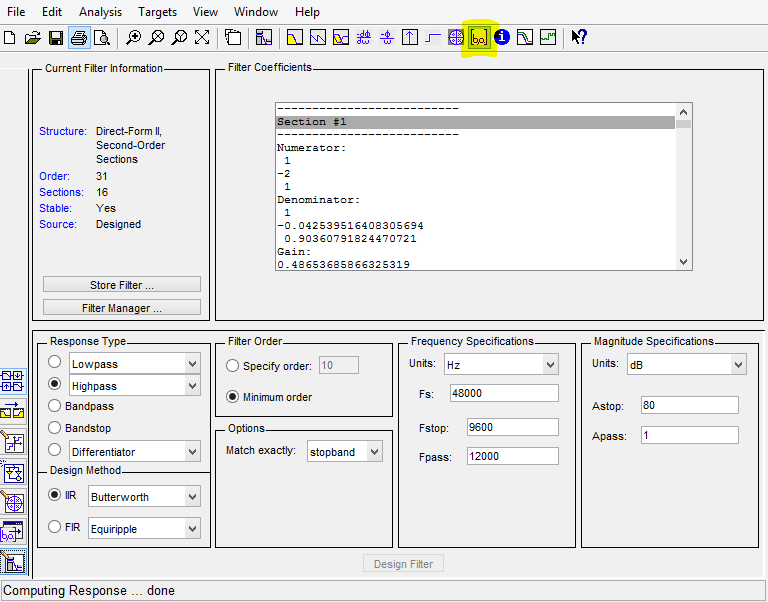
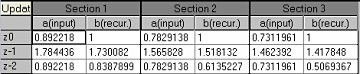
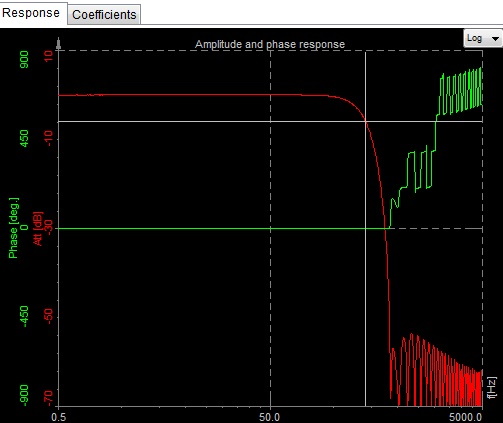
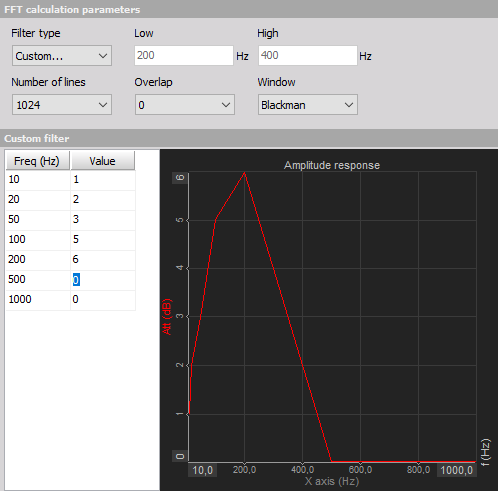
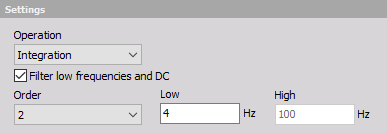
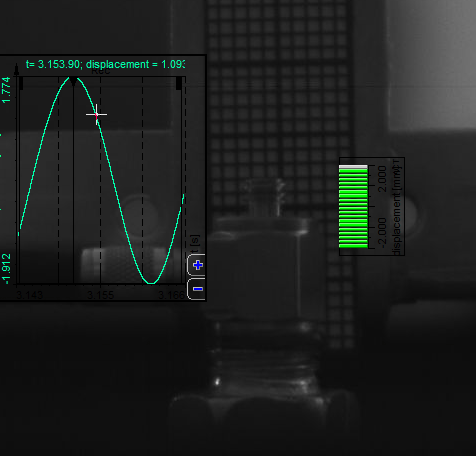
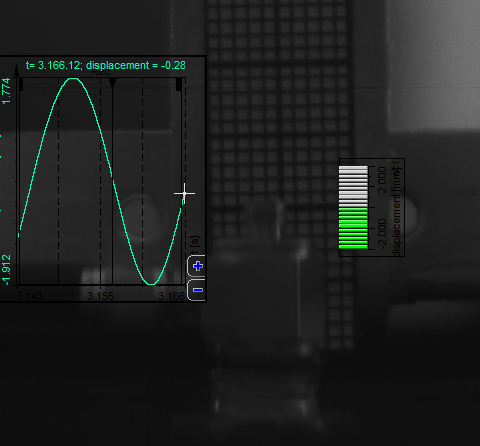
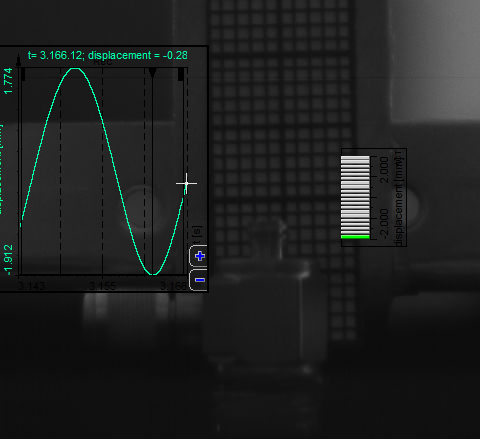
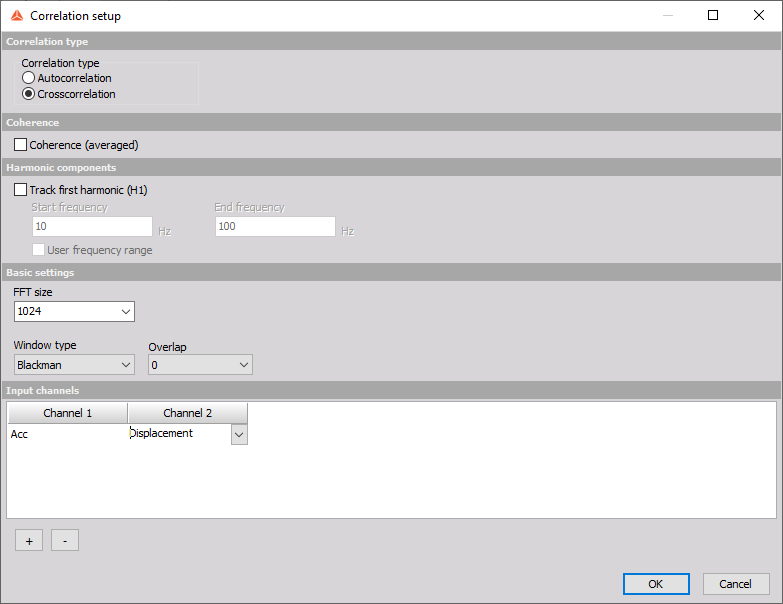
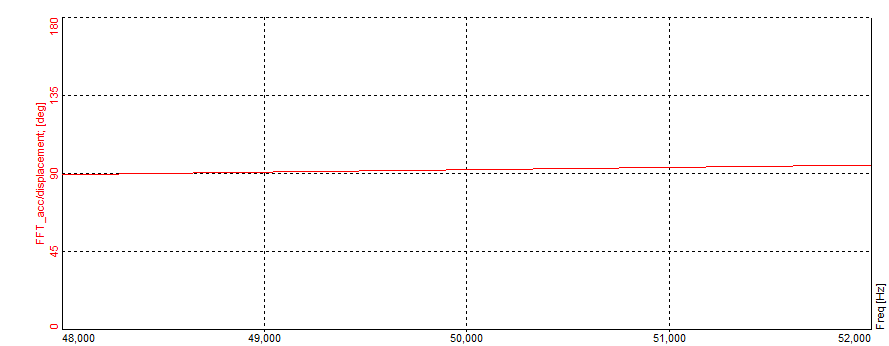
Let's start with some terminology followed by a basic introduction. Then we are going to acquaint ourselves with analog and digital filters, as well as converters and do a comparison of the two. Next on the list will be the different types of filters and their uses. Finally, we are going to see how to setup and use all of these filters in Dewesoft X.
In the field of signal processing, a filter is a device or process that, completely or partially, suppresses unwanted components or features from a signal. This usually means removing some frequencies to suppress interfering signals and to reduce background noise.
Although the task of filters is pretty simple, they are invaluable in today's electronics, particularly in telecommunications.
Terminology
Here is a short list of terms that will be used in this tutorial. Some terms might not be explained here, but will have an explanation later in the text.
- Attenuate - to decrease the amplitude of an electronic signal, with little or no distortion.
- Low-pass filter - a filter that passes low frequencies and attenuates the high ones.
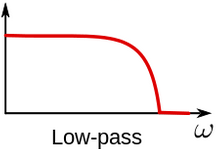
Image 1: Representation of frequency band that is visible after Low-pass filtering
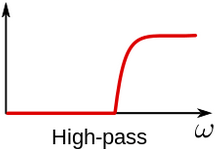
- High-pass filter - a filter that passes high frequencies and attenuates the low ones.

Image 2: Representation of frequency band that is visible after High-pass filtering
- Band-pass filter - a filter that passes only frequencies in a specific band.
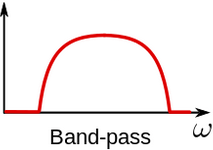
Image 3: Representation of frequency band that is visible after Bandpass filtering
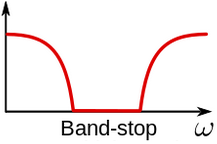
- Band-stop filter - a filter that only attenuates frequencies in a specific band.

Image 4: Representation of frequency band that is visible after Bandstop filtering
- Notch filter - a filter that rejects only a specific frequency (an extreme band-stop filter).
- Comb filter - a filter that has multiple regularly spaced narrow pass-bands.
- All-pass filter - a filter that passes all frequencies, but the phase of the output is modified.
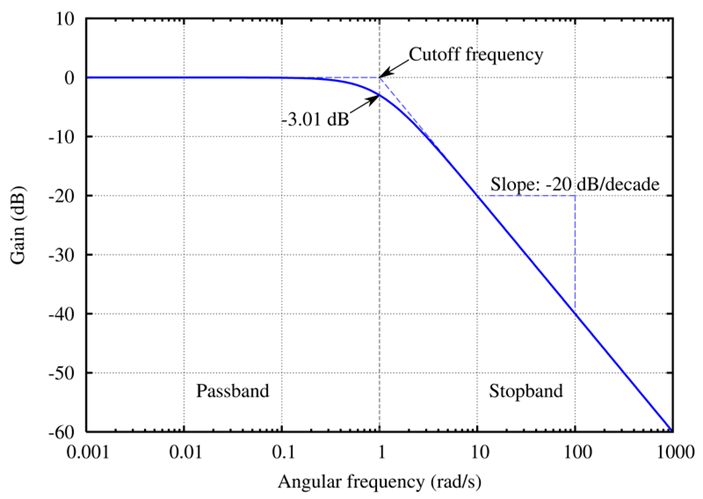
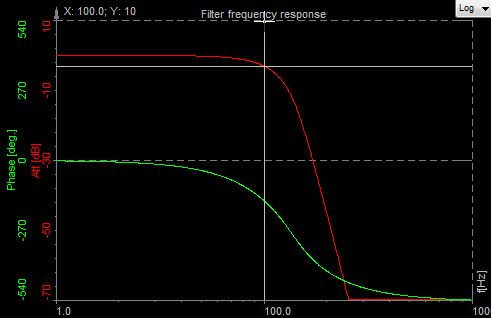
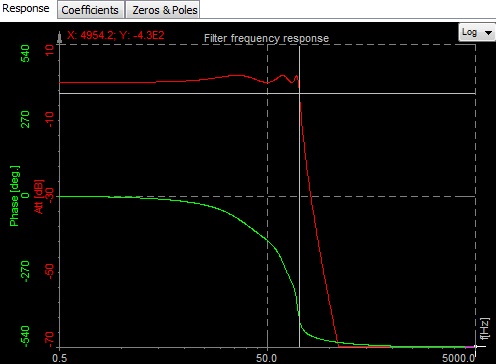
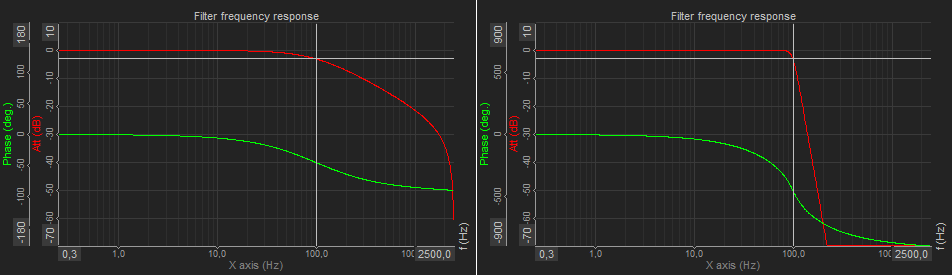
- Cutoff frequency - the frequency beyond which the filter will not pass a signal.
- Roll-off - a rate at which attenuation increases beyond the cutoff frequency. The steepness of the transition between the pass-band and stop-band.
- Transition band - the band of frequencies between a pass-band and stop-band.
- Ripple - the maximum amplitude error of the filter in the passband in dB.
- The order of the filter - the degree of the approximating polynomial (increasing order increases roll-off and brings the filter closer to the ideal response).



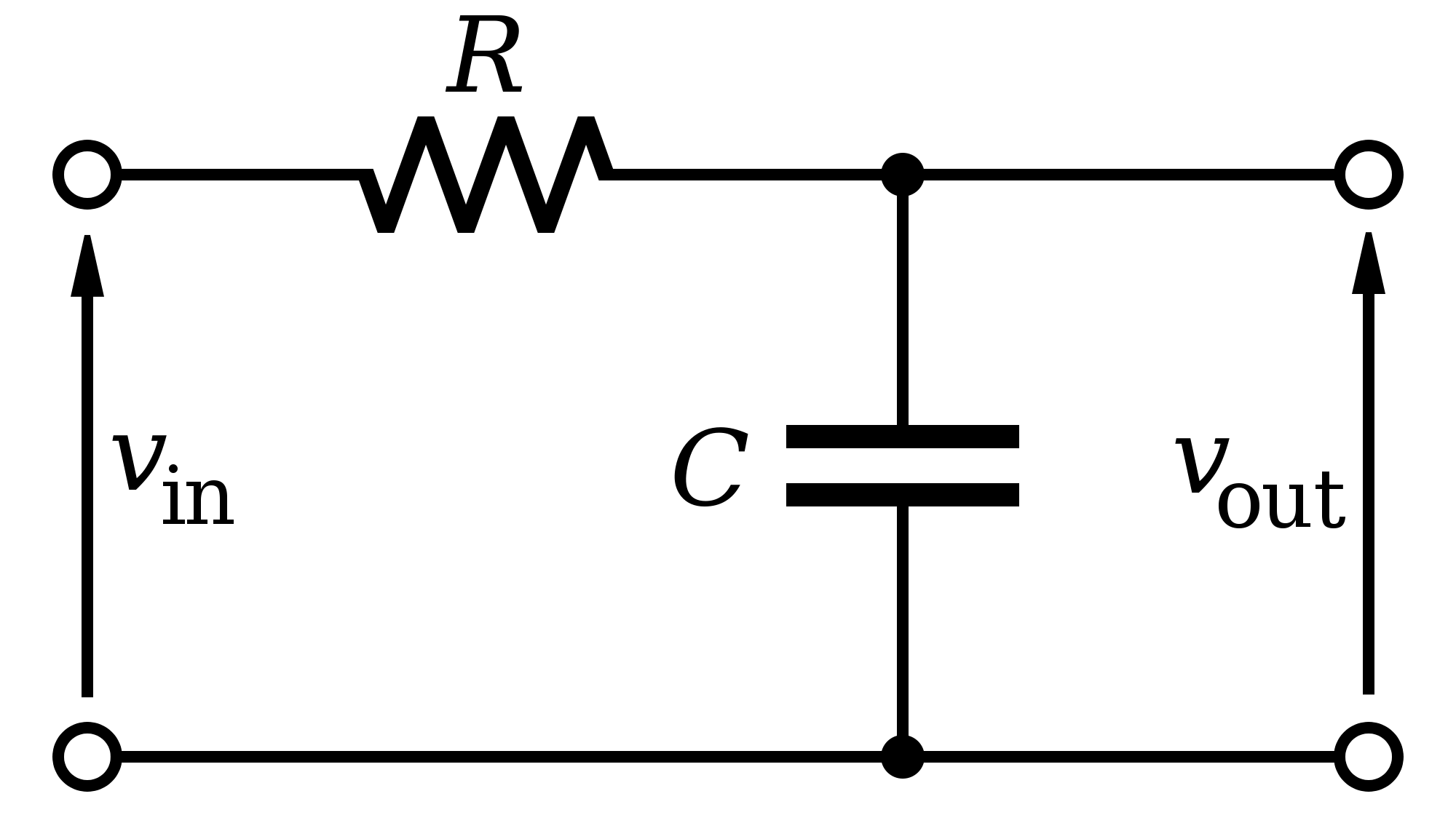





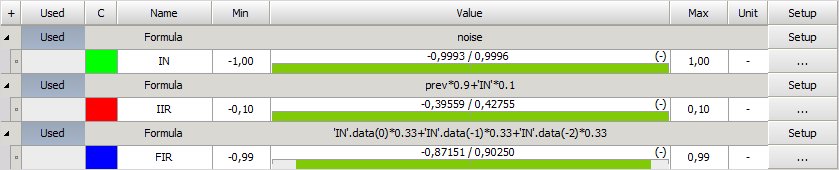

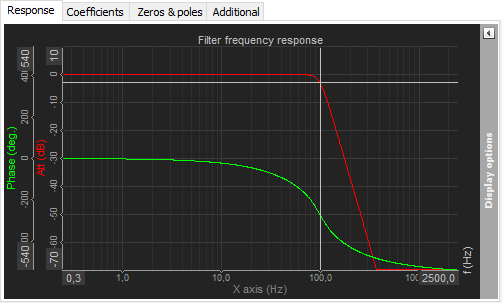
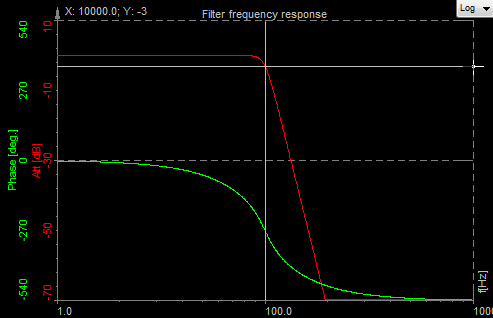
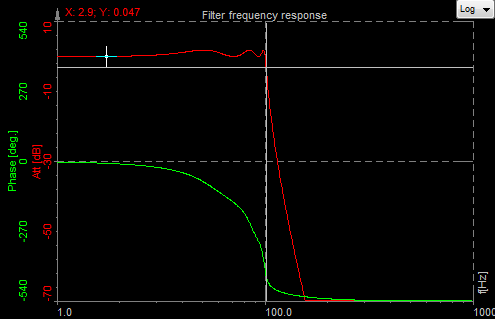
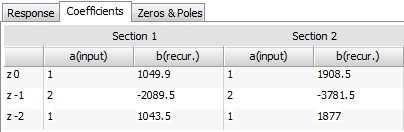
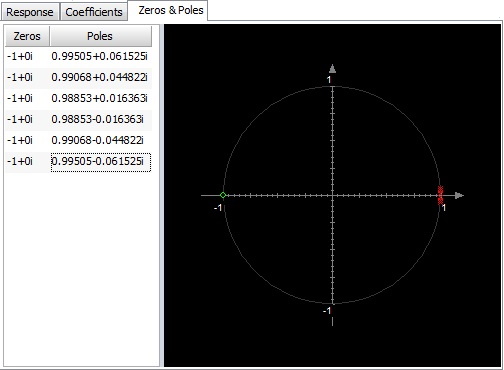
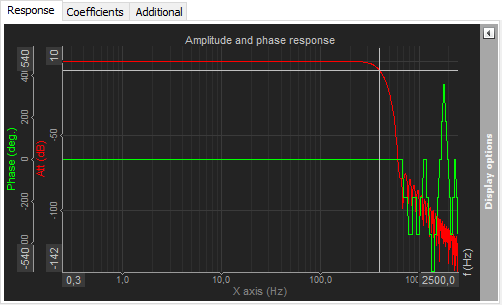







.png)
.png)
.png)
.png)
.png)
.png)