Fundamental symmetrical components
Normally an electric power system operates in a balanced three-phase sinusoidal steady-state mode. Disturbances, for example a fault or short circuit, lead to an unbalanced condition. As the following image depicts on the left-hand side is a balanced system with a symmetrical phase shift and equal vector distances. On the right-hand side is an unbalanced system with an unsymmetrical phase shift and uneven vector lengths.
Image 24: Balanced system and an unbalanced system
By using the method of the symmetrical components, it is possible to transform any unbalanced 3-phase system into 3 separated sets of balanced three-phase components, the positive, negative and zero sequence.
Image 25: Unbalanced system to balanced system transformation
The advantage of the symmetrical balanced system lies in that the calculations are simplified. Should a fault arise or there is a short circuit in the system, an unbalanced system can be transformed into a balanced system with symmetrical components, where the system calculations can be done with the normal formulas that would be used in a balanced system. The calculated values are then transformed back to the unsymmetrical system (real-scenario) phase voltages and currents. In general, a 3-phase system can be depicted and mathematically described as follows:Image 26: Symmetrical system
A balanced 3-phase system looks like the image below with the same RMS-value for all line voltages and currents, and a 120° phase shift between each of them.
Image 27: Symmetrical balanced system vectorscope
In order to explain the basic idea of the symmetrical components, the first step would be to define the operator as a unit vector with an phase angle of 120° or 2*pi/3.
\[ a = e^{\frac {j2\pi}{3}} \]
The voltages can be described mathematically in different ways as the table below shows:
Table 6: Symmetrical components complex and angle calculations Calculation of zero-sequence system
In an symmetrical system the following equation is valid:
\[ U_{L1} + U_{L2} + U_{L3} = 0 \]
In a real system the sum won't be zero. There will be a voltage difference as the following equation shows:
\[ U_{L1} + U_{L2} + U_{L3} = \underline{\Delta} u \]
This voltage difference divided through 3 represents the so called zero-sequence system:
\[ U_0 = \frac {1}{3} \cdot \underline{\Delta} u = u_{10} = u_{20} = u_{30} \]
The zero-sequence systems for the three phases (u10, u20, u30) all have the same amplitude and phase. Therefore, only the value for the zero-sequence system „U_0“ will be shown.
The calculation of the zero-sequence current is analog to that of the voltage equation.
Calculation of positive-sequence system
The positive sequence system has the same rotating direction as the original system (right). This means it will have the same rotating direction of an electrical machine connected to the grid.
\[ \underline {\nu_{1m}} = \frac {1}{3} (\underline{\nu_1} + \underline{a\nu_2} + \underline{a^2\nu_3}) \]
\[ \underline {\nu_{2m}} = \underline{a^2\nu_{1m}} = \frac {1}{3} (\underline{\nu_1} + \underline{a\nu_2} + \underline{a^2\nu_3}) \cdot \underline{a^2} \]
\[ \underline {\nu_{3m}} = \underline{a\nu_{1m}} = \frac {1}{3} (\underline{\nu_1} + \underline{a\nu_2} + \underline{a^2\nu_3}) \cdot \underline{a} \]
As the values of the positive-sequence system for all three phases have the same amplitude (now that they are symmetrical) and has a phase shift of exactly 120°, it's adequate to show only one value. The value for the positive-sequence system in Dewesoft X is called „U_1“.
Calculation of negative-sequence system
The negative sequence system has the opposite rotating direction as the original system (left). This means it will rotate in opposite direction of an electrical machine connected to the grid.
\[ \underline {\nu_{1g}} = \frac {1}{3} (\underline{\nu_1} + \underline{a^2\nu_2} + \underline{a\nu_3}) \]
\[ \underline {\nu_{2g}} = \underline{a\nu_{1g}} = \frac {1}{3} (\underline{a\nu_1} + \underline{\nu_2} + \underline{a^2\nu_3}) \]
\[ \underline {\nu_{3g}} = \underline{a^2\nu_{1g}} = \frac {1}{3} (\underline{a^2\nu_1} + \underline{a\nu_2} + \underline{\nu_3}) \]
As the values of the negative-sequence system for all three phases have the same amplitude (now they are symmetrical) and has a phase shift of exactly 120°, it's adequate to show one value. The value for the negative-sequence system in Dewesoft X is called „U_2“.
Matrix of zero, positive and negative-sequence system
According to the following equations the phase voltages and currents are transformed into the symmetrical components. The result are three balanced 3-phase systems, the positive (U1, I1), negative (U2, I2) and zero sequence (U0, I0).
Table 7: Matrices of the zero-,positive-, and negative sequence system
As illustrated in the following images, an unbalanced system can be rectified using the positive, negative and zero symmetrical components. The image below depicts an unsymmetrical system as a screen shot taken from Dewesoft X.
Image 28: Unbalanced system vectorscope in Dewesoft X
This screen was provided by Kurt STRANNER (KNG Netz GmbH)
The following image depicts a screen-shot showing the three systems (positive, negative and zero) of the symmetrical components in Dewesoft X:
Image 29: Unbalanced system to balanced system transformation in Dewesoft X
This screen was provided by Kurt STRANNER (KNG Netz GmbH)
Out of the parameters of the symmetrical components (positive-, negative- and zero- sequence) the original system can be rebuilt easily, e.g.:
\[ U_{L1} = U_0 + U_1 + U_2 \]
The following variables are calculated in Dewesoft X and show the components of the zero- and negative-sequence system compared to the positive-sequence system (for the total and the fundamental harmonic).
Table 8: Zero-,positive-, and negative sequence system calculations in the power module Extended positive sequence parameters (according to IEC 614000)
The following calculations are based on Annex C of IEC 61400-21.
Based on the measured phase voltages and currents, the fundamental's Fourier coefficients are calculated over one fundamental cycle T as first step.
\[ u_a, cos = \frac{2}{T} \int_{t-T}^t u_a(t) cos (2 \pi f_1 t) dt \]
\[ u_a, sin = \frac{2}{T} \int_{t-T}^t u_a(t) sin (2 \pi f_1 t) dt \]
It is important to mention that the index a stands for the line voltage L1. The coefficients for L2 (ub) and L 3 (uc) as well as the coefficients for the currents (ia, ib, ic) are calculated exactly the same. Furthermore f1 is the frequency of the fundamental. The RMS value of the fundamental line voltage is:
\[U_{a1} = \sqrt {\frac {u^2_{a,cos} +u^2_{a,sin} } {2}} \]
Table 9: Extended positive sequence calculations in the power module Extended negative sequence parameters (according to IEC 614000)
Table 10: Extended negative sequence calculations in the power module
Extended zero sequence parameters (according to IEC 614000)
Table 11: Extended zero sequence calculations in the power module
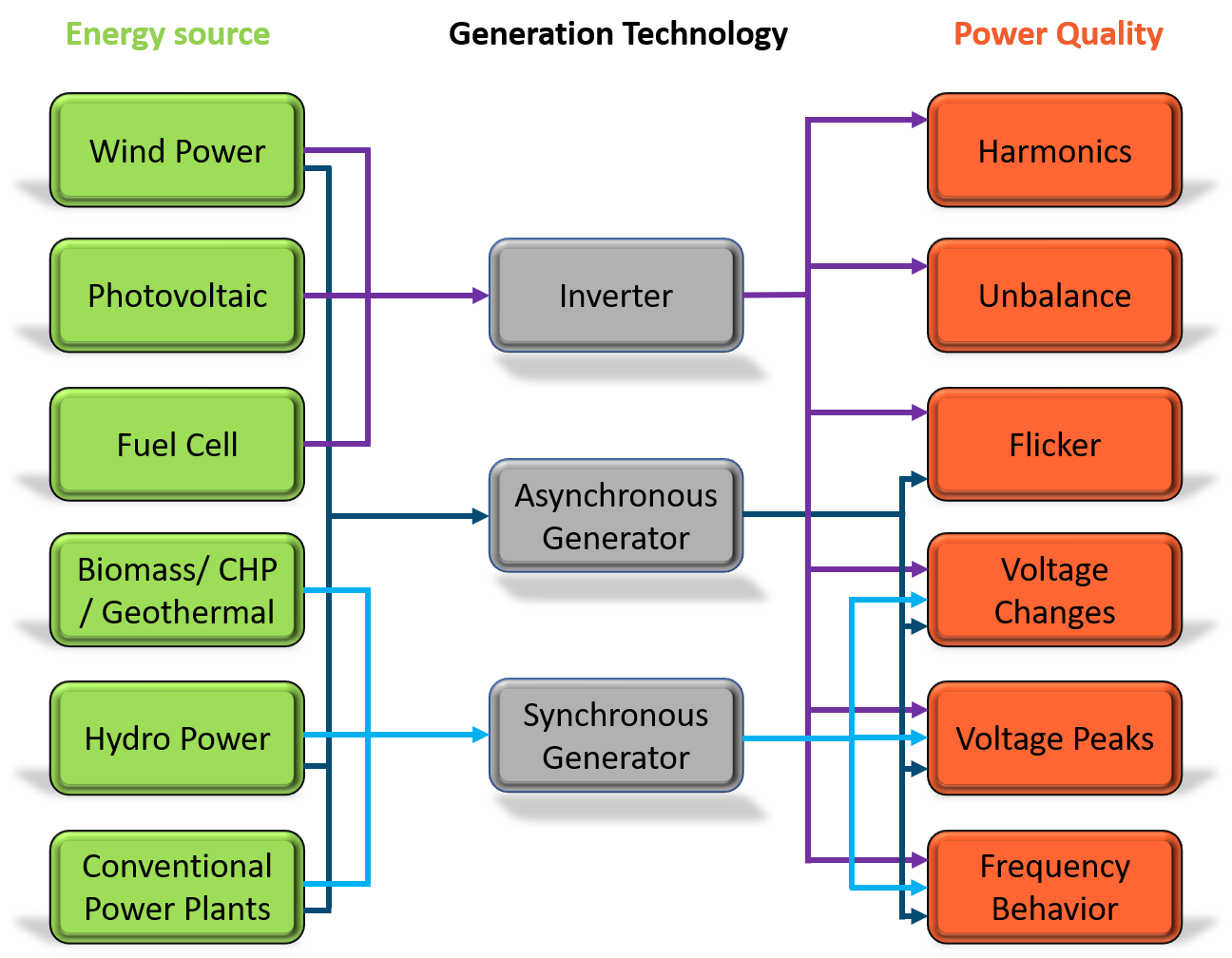Image 1: Power quality application overview
